Важная информация
АВАРИЙНОСТЬ НА ДОРОГАХ РОССИИ
За прошедший год в России произошло 199 431 ДТП, что на 2,1% меньше, по сравнению с предыдущим годом. В них погибло 26 567 (-3,9%) человек, а 250 635 (-1,9%) человек получили ранения различной тяжести.
11845 (-3,9%) ДТП произошли по вине водителей, находившихся за рулем в состоянии алкогольного или наркотического опьянения. В результате этих ДТП 1 954 (-15,4%) человека погибли, а 17 280 (-4,6%) человек получили ранения.
Как видно из полученной таблицы, тарифы на услуги пассажирского транспорта по Тверской области постоянно увеличиваются (или в лучшем случае остаются на уровне предыдущего года). Я считаю, что повышение тарифов и так при уменьшающемся количестве пассажиров нецелесообразно, и тут можно найти другие пути окупаемости перевозок, нежели повышение тарифов.
Как известно, работа любого транспорта требует затрат энергии – будь то бензин, электроэнергия или дизельное топливо. Рассчитаем средний уровень расхода автомобильного бензина и дизельного топлива следующего ряда:
Табл. 4. Потребление автобензина и дизельного топлива автотранспортом организаций всех отраслей экономики (тыс. тонн)
|
2000 |
2001 |
2002 |
2003 |
2004 | |
|
Автомобильный бензин |
94,0 |
91,3 |
98,7 |
89,6 |
87,4 |
|
Дизельное топливо |
62,8 |
62,0 |
57,8 |
56,2 |
55,8 |
Причём видно, что это интервальный ряд с равными интервалами. Следовательно, средний уровень считаем по следующей формуле: 
, где n – число периодов, yi – уровень i-го года. Получаем средние уровни:
Для автомобильного бензина: ỹ = 92,2
Для дизельного топлива: ỹ = 58,9
Т.е. автомобильного бензина с 2000 по 2004 года потреблялось, в среднем, около 92,2 тыс. тонн, а дизельного топлива меньше – 58,9 тыс. тонн.
Теперь рассчитаем среднегодовые показатели роста по формуле: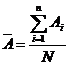 
, где Ai – значение цепного прироста, N – количество приростов. В результате имеем: 
-1,65 (для автомобильного бензина) и -1,75 (для дизельного топлива). Т.е. в среднем, в год потребление бензина падает на 1,65 тыс. тонн, а дизельного топлива – на 1,75 тыс. тонн.
Также рассчитав темпы роста по формуле 
= 
, где N – число коэффициентов роста, Трi – цепные Тр (i=
), получаем, что в среднем, в год потребление бензина падает примерно на 2%, а дизельного топлива – на 3%. Для большей наглядности построим столбиковую диаграмму:
Диаграмма 1.
Динамика потребления дизельного топлива
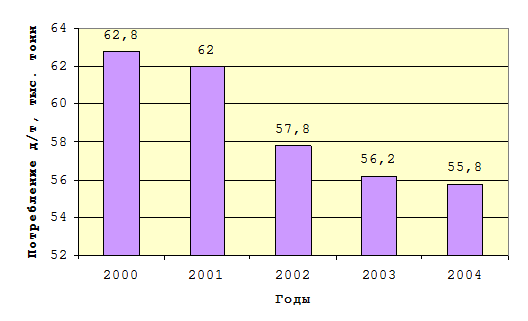
Из этой диаграммы видно, что потребление дизельного топлива имеет непрерывную тенденцию к падению.
Теперь проведём корреляционно-регрессионный анализ для изучения связи между изучаемыми явлениями, т.е. выявление наличия связи и определения её силы. Т.е. построим и проанализируем экономико-математическую модель в виде уравнения регрессии, т.е. в виде той или иной функции, приближённо выражающей зависимость среднего значения результативного признака от одного или нескольких факторных признаков.
В качестве результативного признака возьмём количество автомобилей у индивидуальных владельцев по районам Тверской области, а в качестве факторного – количество человек, проживающих в этих районах.
Коэффициент а1 рассчитывается по формуле: 
, где xi и yi – значения соответствующих признаков, 
и 
– соответствующие значения этих признаков; а коэффициент а0 – по формуле: 
. Коэффициент корреляции определяется по формуле: 
.
После проведённых расчётов получаем модель следующего вида:
y = 2791,36 + 22,66*х
Т.е. при изменении численности населения на 1%, количество автомобилей увеличивается примерно на 22 штуки.
Коэффициент корреляции получился равным ≈ 41%, что означает, что между признаками существует средняя связь.